10-2

공개키암호 응용 방식

Encrption & Decryption
- 메시지암호화
Digital Signature
- 전자서명
Key exchange
- 암호화에 사용되는 세션키 전달 용도
- 하이브리드 방식 - key encapsulation
- src가 메시지 암호화하는것처럼 세션키를 암호화해서 보내면 dest가 세션키 확인 가능

Discrete logarithm

디스크리트 로그 문제

a가 2일때 몇 번 제곱하면 15가 나올까?

답 : 11

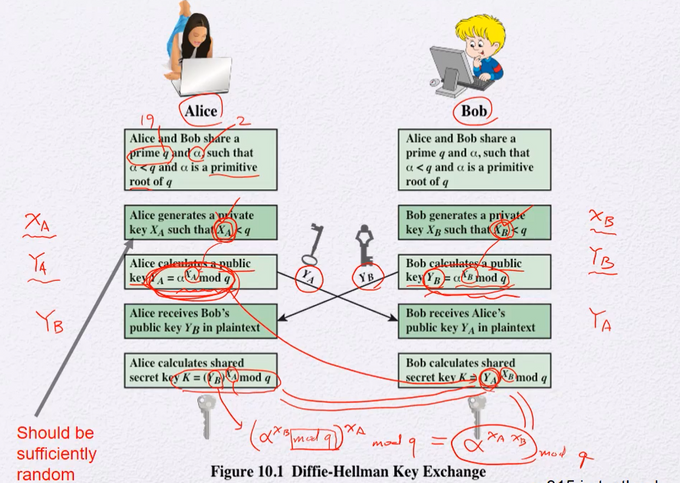
Diffie-Hellman Key Exchange

디스크리트 로그 문제가 어렵다는 것을 응용

p가 19, 알파가 2

Alice와 Bob의 p와 알파를 공유한다 (퍼블릭함)
Alice는 랜덤키 XA(pr)를 생성
Bob도 랜덤키 XB(pr) 생성
각자 YA와 YB 생성(pb)
YA와 YB를 서로 공유
받은 상대의 퍼블릭키를 자신의 프라이빗키로 제곱한 후 mod q를 하면 둘은 동일한 값의 키 K를 얻을 수 있다
어떻게 두 K가 같을 수 있는가?
- YB 는 알파의 XB제곱
- Alice는 YB에 XA 제곱을 해야하니 결국 알파의 XB제곱에 XA제곱을 하는 셈
- Bob또한 YA에 XB 제곱을 하니 결국 알파의 XA 제곱 XB제곱을 하는 셈
- 즉 둘의 K는 알파^(XA x XB) mod q로 값이 같다
여기서 왜 디스크리트 로그 문제가 중요한걸까?

모두에게 알파, q, YA, YB 값이 공개됨

프라이빗키인 XA는 YA를 구할 때 알파의 지수로 사용되므로 디스크리트 로그 문제를 쉽게 풀 수 있다면 프라이빗키인 XA도 알아낼 수 있음
결론은, 디피헬먼 알고리즘에서 안전성을 보장하려면 XA와 XB를 알아낼 수 없어야함
만약 Alice가 XA를 잘못 생성하면 공격가능
- XA는 랜덤으로 생성됨 - 난수발생기의 성능이 중요
- 만약 Alice가 시간값같은걸로 랜덤 시드를 발생시킨다면 위험. 공격자가 시간대를 추측가능
- seed가 뭐냐에 따라서 안전성이 걸림
- 위에서 YA와 q, 알파값으로 XA를 추측해내는 방법이 아니라 가능성 높은 XA들을 추측해서(ex. 시간대) 모든 XA후보들로 계산을 해서 진짜 XA를 맞춰버릴수도있음

RSA vs DH : Forward Secrecy

RSA : Key Encapsulation 해서 한 쪽이 세션키 전달

DH : 양쪽에서 공유

둘의 차이는 Forward Secrecy

RSA

두 개의 세션이 있다고 가정

앨리스가 세션키를 밥의 퍼블릭키를 사용해서 암호화하면,

밥이 자신의 프라이빗키로 암호문을 복호화해서 세션키 획득

둘은 세션키를 가지고 AES 알고리즘을 써서 메시지 주고받음

만약 세션 2때 해킹으로 밥의 프라이빗키가 노출된다면?
공격자또한 밥의 프라이빗키로 세션키 획득이 가능해짐! (세션 1의 키와 세션 2의 키 모두 획득 가능)
메시지의 AES 알고리즘을 세션키로 풀 수 있어서 공격자는 세션1,2의 메시지 내용을 전부 볼 수 있음
즉, 한 번 프라이빗키가 뚫리면 모든 세션의 메시지가 노출됨

DH

두 개의 세션이 있다고 가정

각자 프라이빗키인 XA, XB를 만들고 그걸로 퍼블릭키인 YA, YB를 생성해서 공유

공유한 퍼블릭키로 세션키 생성

세션키를 생성했다면 XA와 XB는 필요가 없으니 삭제해도 됨

만약 세션 2때 해킹으로 밥의 프라이빗키가 노출된다면?
공격자는 XB를 사용해서 세션 2의 세션키를 획득 가능
그러나 세션 1때 사용한 XB는 이미 삭제되었기 때문에 세션 1때 주고받은 메시지는 훔쳐볼 수 없음
즉, 이전 세션의 메시지는 안전함

Forward Secrecy

앞 쪽은 안전하다는 말

RSA와 DH의 차이는 Forward Secrecy다

RSA는 프라이빗키가 뚫리면 모든 세션의 메시지가 노출된다

DH는 프라이빗키가 뚫리면 해당 세션의 메시지만 노출되지만 이전 세션의 메시지는 안전하다

RSA도 Forward Secrecy 할 수는 없을까?

DH에서 사용한 XA, XB를 삭제해버려 이전 세션의 키를 복구할 수 없게 만든것처럼, RSA의 프라이빗키인 d도 사용하면 삭제하고 매 세션마다 다시 새로 만들자!

근데 키페어 만드는 과정이 개 복잡함. 추천하지않는 방법. 비효율적
그냥... DH쓰자...^^
- TLS 1.3에서는 아예 RSA의 key exchange지원안함 (1.2까지만 지원)

Man in the Middle (MitM) Attack

중간에서 src or dest 인척 속임
공격자인 다스는 앨리스에겐 밥인척 YD1을 보냄
밥에겐 앨리스인척 YD2를 보냄
사실상 앨리스 - 다스, 밥 - 다스 사이 정상적인 DH가 작동되긴했지만 상대가 다스라는게 문제
다스가 중간에서 메시지를 정상적인척 전달해주기때문에 앨리스와 밥은 중간에 다스가 있는지 모름

dest는 받은 퍼블릭키 Y가 src가 보낸 Y가 맞는지 확인할 방법이 없기 때문에 발생하는 문제
- 공인 인증서로 해결 가능

ElGamal Encryption

디스크리트 로그 문제에 기반한 또 다른 암호임

퍼블릭한 파라미터 q와 알파 생성

Key Generation by Alice

DH처럼 XA 랜덤으로 생성
XA로 YA생성
- DH와의 차이 : DH는 세션키 생성을 위해 X와 Y를 임시로 만들지만 Elgamel은 이렇게 생성한 키페어를 지속적으로 사용함

Encryption by Bob (with Alice의 PB)

밥은 랜덤한 정수 k를 생성
밥은 앨리스의 퍼블릭키 YA와 k를 가지고 K를 생성
알파와 k를 가지고 C1생성
K와 평문M을 가지고 C2생성
두 개의 암호문 C1, C2를 앨리스에게 전달!

Decryption by Alice (with Alice의 PR)

C1 - 밥의 임시 공개키라고 볼 수 있음

앨리스는 자신의 프라이빗키와 C1을 가지고 K를 복원
앨리스는 복원한 K와 C2를 가지고 본래의 메시지로 복호화

DH와 OTP을 합친거라고 볼 수 있음

One Time Pad (랜덤키)

메시지와 같은 길이의 랜덤키 K를 생성 - OTP의 키처럼 사용

Elliptic Curve Arithmetic

타원곡선암호

3072 bit의 RSA와 128bit AES의 안전성이 비슷함

큰 비트수의 암호를 쓰면 계산도 많이 해야하고 메모리도 많이 사용하고...

그 대안이 ECC (Elliptic Curve Arithmetic)

공개키 암호의 표준 IEEE P1363a에 타원곡선 암호가 포함됨
자동차 환경 무선통신(WAVE) 표준 IEEE 1609에서 rsa는 배제되어있고 타원곡선만 언급됨
대부분의 공개키암호 표준에서는 디피헬만, rsa, 타원곡선암호 다 포함되어있음. 최근에 나오는 특정 표준에서는 타원 곡선 암호만 포함하게 하는 경우도 있음
같은 안전성을 주기위해서 훨씬 짧은 키를 써도 된다 (같은 키 길이를 쓰면 ECC가 훨씬 안전함)
자동차의 경우 패킷 길이가 길면 그 사이 차가 슝 지나가 통신 범위에서 멀어져 전송을 못할수도있다. 즉, 패키 길이가 짧은게 중요
패킷 길이가 작아야하는데 3072bit인 RSA는 적합하지않음 (타원곡선 암호는 256bit로 같은 안전성을 보여줌)

Comparable Security Strengths

타원곡선암호와 기존 공개키 암호의 비교

NIST에서 표준화한 키 관리 권고사항에 대한 표준 (가장 최근의 Revision 5)

보안강도 : 공격자가 성공적으로 키를 복구하기위해 어느정도의 작업을 해야하는가? - 클수록 좋음

80이라고하면 공격자의 작업량이 2^80이라는 뜻

128과 256을 비교하면, bit수는 두 배가 됐지만 공격자의 작업량은 2^128배만큼 늘어남

rsa나 디스크리트 로그 계열 암호들은 모듈러스에 비해 훨씬 적은 안전성을 제공하게 된다

타원곡선은 공격자에게 요구되는 비트수의 두 배정도되는 숫자를 키로 쓰면 안전하다

같은 비트 (Security Strength)안전성을 봤을 때 RSA에 비해 타원곡선에게 요구되는 비트의 수가 훨씬 적다. 증가하는 속도도 더 낮음.

Abelian Group

아래 조건들을 만족하는 원소들의 집합

Cyclic Group

어떤 제너레이터가 그룹 안의 모든 원소를 생성해낼 수 있는 그룹.

타원 곡선

y에 대해서는 2차식이고 x에 대해서는 3차식으로 되어있는 곡선

두 가지 형태 존재
- 타원이 있고 나머지는 곡선으로 떨어져있는 형태
- 곡선 하나로 다 이어져있는 형태

ECDLP(Elliptic curve discrete logarithm problem)

타원곡선 암호는 ECDLP에 기반하고있다

그래프 내 어떤 점 P와 ,Q를 이어서 직선을 그으면 또 다른 점, -(P+Q)와 만난다 (3차 그래프이기때문)

x 중심축을 기준으로 -(P+Q)와 대칭되는 점이 (P+Q)이다

서로 다른 점 P+Q외에 같은 점 P와 P를 더한 2P도 얻을 수 있다.

두 점 P와 Q를 이어서 그은 직선이 아닌 P를 접하는 직선을 그음

위 방법으로 2P, 3P, 4P ... 계속 구하기 가능 (계속 더 하다 보면 언젠가 자기자신 P로 돌아옴)

즉, P하나로 모든 원소를 생성하는 Cyclic Group을 나타낼수도있음

디스크리트 로그 문제와 비슷하게 활용할 수 있음
- kP = Q 일 때,
- k와 P가 주어지면, square & multiply처럼 덧셈과 2배연산을 반복해서 Q를 계산해낼수있다
- 그러나 반대로 P와 Q가 주어졌을 때 k를 알아내기는 힘들다
타원곡선의 Addition이 finite field의 modular mulitiplication처럼 작동할 예정
Multiple addition이 modular exponentiaion처럼 작동함
디스크리트 로그문제보다 더 어려움

ECDH (Elliptic Curve Diffie-Hellman) Key Exchange

기존의 지수연산을 타원곡선 점들간의 몇 배 연산으로 대체할 수 있음

즉, 디스크리트 로그 상에서 정의되는 여러가지 프로토콜들을 그대로 사용할 수 있다

디피헬먼도 타원곡선 버전으로 만들 수 있음

E : 타원 곡선식

G : 제너레이터. 어디서부터 시작할 것인지

n : G로 만들 수 있는 가장 큰 값

User A Key Generation

n보다 작은 nA(PR)를 랜덤하게 뽑는다

nA x G 를 해서 PA(PU)를 구한다

User B Key Generation

위와 마찬가지로,

n보다 작은 nB(PR)를 랜덤하게 뽑는다

nB x G 를 해서 PB(PU)를 구한다

둘은 PA와 PB를 서로에게 공유한다
둘은 받은 상대의 퍼블릭키(P)와 자신의 프라이빗키(n)를 곱해 K를 만든다

공격자는 E, G, PA, PB를 알아도

nA, nB를 추측해내기 어렵다.

여기서 사용하는 nA, nB가 이전에 했던 XA, XB보다 작은 bit의 수이다. 훨씬 효율적!

Security of Elliptic Curve Cryptography

ECDLP를 깨는 가장 효율적인 알고리즘은 Pollard rho method, DLP에도 똑같이 적용됨

DLP는 Pollard rho method처럼 일반적인 방법보다 더 빨리 문제를 풀 수 있는 알고리즘이 존재 (팩토링이랑 비슷?)

보통 키길이가 비슷하면, rsa나 dh나 타원곡선암호든 계산량이 비슷함.

키의 길이가 작으면 계산량이 작다는 뜻

그럼, 비슷한 시큐리티를 가정했을 때 타원곡선쪽이 다른 방법보다 더 적은 계산량을 제공하고 효율성을 자랑한다.