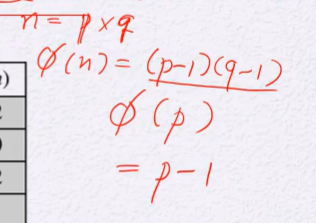Divisibility
`a/b` = `a=mb` = `b|a`b는 0이 아니다
b는 a의 divisor, a는 b의 multiple
ex) 17|0, -5|30
- a|1 이면 a는 ±1
- a|b, b|a 이면 a = ±b
- 0이 아닌 모든 정수 b는 0의 약수가 된다 ( 나머지가 0이긴하니까... )
- b|g and b|h 이면 b|(mg + nh)
Division Algorithm
a = qn +r 일 때
0 ≤ r < n;
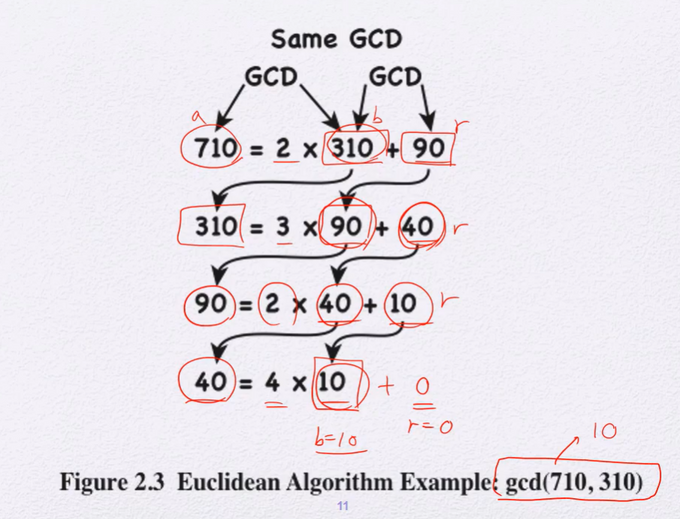
q = [a/n] (작거나 같은 수 중 최대)📌 Euclidean Algorithm : for GCD
for GCD
gcd(a,b) -> gcd(b, a mod b)
a>b 일 때, r이 0이 될 때까지 반복한다
모듈러 연산
a = qn +r
0≤ r < n-11 mod 7 = 3
-11 = 7*-2 +3
📌 합동(congruent)
(a mod n) = (b mod n)
-> a ≡ b (mod n) : 우와! 합동이다!
만약 a ≡ 0 (mod n)이라면, n|a이다.
-> a를 n으로 나눴을 때 나머지가 0이라는 뜻이므로
ex)
73 ≡ 4 (mod 23)
: 73을 23으로 나눴을 때의 나머지와 4를 23으로 나눴을 때의 나머지가 같다
21 ≡ -9 (mod 10)
📌 Properties of Congruences
- a ≡ b (mod n) iff n|(a-b)
- a ≡ b (mod n) 이면, b ≡ a (mod n)
- a ≡ b (mod n) & b ≡ c (mod n) 이면, a ≡ c(mod n)
1번 증명 : 만약 n | (a-b) 이면 (a-b) = kn
-> a = b + kn
(b + kn) mod n= b mod n
따라서 a mod n = b mod n, 즉 a ≡ b(mod n)
📌 Modular Arithmetic
- [(a mod n) + (b mod n)] mod n = (a + b) mod n
- [(a mod n) - (b mod n)] mod n = (a - b) mod n
- [(a mod n) * (b mod n)] mod n = (a * b) mod n
증명
a = r1 + jn,
b = r2 + kn 이라고 할 때
(a+b) mod n = (r1 + jn + r2 + kn) mod n
= ( r1 + r2 +(j+k)n ) mod n # mod n 에 의해 (j+k)n 은 0이 된다.
= ( r1 + r2 ) mod n
= a (mod n) + b (mod n)
📌 Arithmetic Modulo 8
항등원 : 연산을 해도 처음 값과 똑같이 나오게 해주는 수
덧셈의 항등원 : 0, 곱셈의 항등원 : 1
📌 역원 : 연산을 했을 때 항등원이 나오게 해주는 수
덧셈의 역원은 모든 수에게 있지만 곱셈의 역원은 특정한 수에게만 있다
곱셈의 역원이 존재하려면 Modulo와 서로소여야한다.
덧셈의 역원 : [ a + (역원) ] mod n = 0
ex) modulo 8에서 3의 역원은 5이다 : (3+5) mod 8 = 0
곱셈의 역원 : [ a * (역원) ] mod n = 1
ex) modulo 8 에서 5의 역원은 5이다. : (5*5) mod 8 = 1
Properties of Modular Arithmetic for Int in Zn
Z : 모든 정수의 집함
Zn : Z를 n으로 나눴을 때 나머지가 되는 정수들의 집합
= {0, 1, 2, ... , n-1}
교환 법칙, 결합 법칙, 분배 법칙, 항등원, 역원
(곱셈의 역원은 있을 수도 있고 없을 수도 있으니 정의되어있지않음)
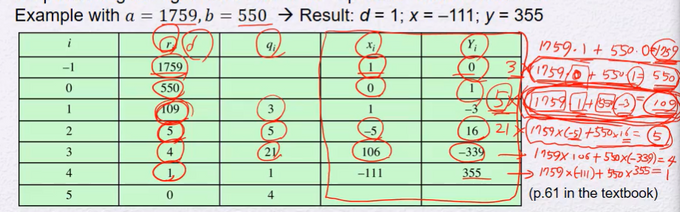
📌 Extended Euclidean Algorithm : for 곱셈의 역원
for 곱셈의 역원modulo 1759에서 550의 곱셈의 역원은 355이다
modulo 550에서 1759의 곱셈의 역원은 439이다
원래 1759 * -111 이지만 -111은 음수이므로 -111을 mod 550해서 양수로 만든다
-111 mod 550 = 439
📌 Fermat's Theorem
prime numbers
어떤 정수 a는 (n제곱 형태의 ) prime numbers들의 곱 형태들로 표현할 수 있다
편의상 앞으로 prime number를 p로 나타내겠음
-
p는 prime이고 a는 p로 나눠지지않는 양의 정수일 때 :a와 p가 서로소
a mod p = 0
a(^p-1) mod p 를 했을 때 1이 나옴
-
p는 prime이고 a는 양의 정수
a(^p) ≡ a (mod p)
Euler totient function
1부터 n까지의 양수 중 n과 서로소가 되는 수들의 개수
p와 q가 prime number라면 서로소가 되는 수들의 개수는 p-1, q-1이다
Primality test
prime인지 아닌지 test
Trial division
처음부터 무식하게 다 나눠보기
Fermat test
확률적인 방법
페르마의 정리 : 만약 p가 prime이고 a와 p가 서로소라면,
무조건 a(^p-1) ≡ 1 (mod p) 이다. (a는 유클리드 알고리즘을 사용해 구한다)
a(^p-1) ≡ 1 (mod p) 가 아니라면 p는 prime이 아니다
a(^p) ≡ a (mod p)
왜냐면 a(^p-1) 였을 때 mod p 하면 1이었으니까 ...
그 1에다가 a곱하고 mod p하면 a가 나올 수 밖에 없음 (둘이 서로소니까 나눠질 가능성은 0)
Miller-Rabin test
- Fermat test (기본적으로는 페르마 테스트)
-
NSR (nontrivial sqare root) test (에 추가)
x² mod n = 1이 참일 때 x가 1 또는 n-1이 아니라면 n은 prime이 아니다
ex) 4² mod 15 = 1 , 그러므로 15는 prime이 아니다
Deterministic algorithm
miller-rabin은 틀릴 확률이 조금이지만 있음. trial처럼 100%맞는 알고리즘은 없을까?
AKS 알고리즘
trial보다는 빠르지만 miller-rabin보다 느림
Hybrid
ex) trialdivison + MR/Fermat
prime인지 test할 수 n을 루트n까지 다 하지하고 어느정도만 trial division을 수행하다가 어느정도까지 수행을 했으면 MR/Fermat로 넘어가는
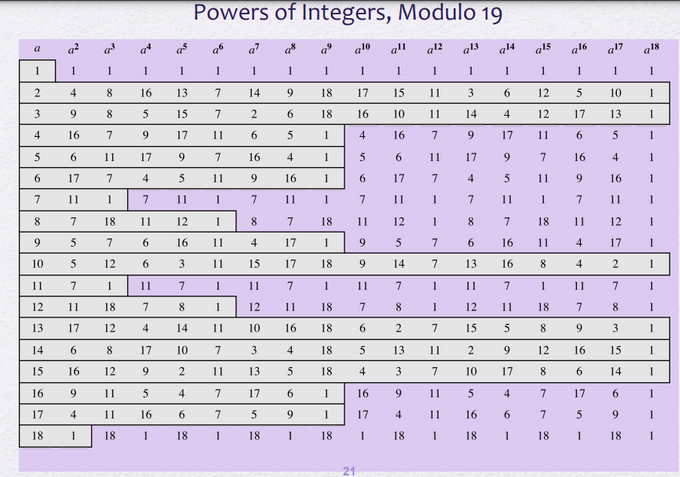
📌 Power of Integers, Modulo 19
거듭 제곱
- 페르마의 정리에 의해 18제곱에서는 모두 1
a(^p-1) ≡ 1 (mod p) - 수마다 특정 사이클이 존재한다
- 사이클 내 중복인 수는 존재하지 않는다
- 18까지 사이클이 유지되는, 사이클내에 1부터 17까지 전부 있는 수들은
generator라고 부른다. ex) 2, 3, 10, 13, 14, 15 generator의 n제곱 형태인 수들은generator의 사이클을 축약해서 가지고 있다-
이전 mod 결과값?에 a를 곱해서 바로 다음의 mod 결과값을 구할 수 있다.
ex) 2를 예시로 볼 때 2의 5제곱 mod 19값인 13에서 바로 2를 곱한 26을 mod 19하면 2의 6제곱 mod 19값인 7이 나온다.
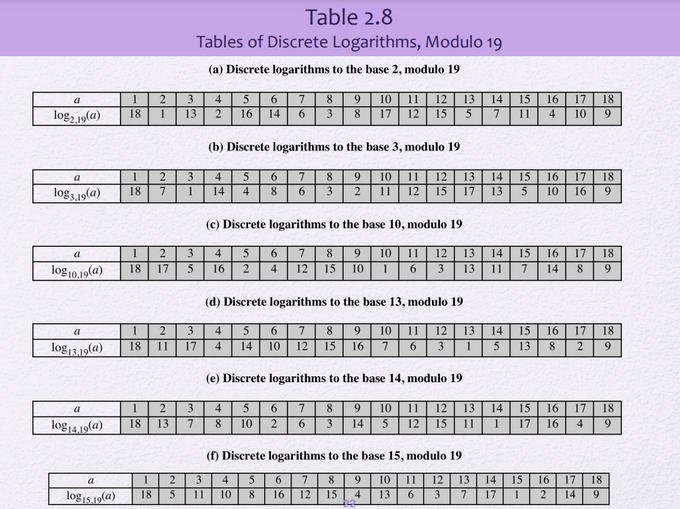
📌 Discrete log
ex) 2와 17과 19를 인자로 주고 (2^n) mod 19 = 17일 때, n은 몇인가? 를 구하는 것을 디스크립트 로그라고한다. : 답은 10
이후 정수 소인수분해와 디스크리트 로그에 기반한 암호화가 나옴
수학적으로 풀기 어렵기 때문