Groups
두 가지에 대한 순서쌍
어떤 연산과 집합으로 합쳐서 정의
· 연산은 +도 될 수 있고 *도 될 수 있음.
+일 경우엔 additive 그룹이라 부르고 * 경우엔 multiplicative 그룹이라고 부름
그룹을 만족시키는 필수 성질
Closure: 닫혀있음
G안에 있는 a와 b가 있을 때 그 둘을 연산한 (a · b) 도 G안에 있어야한다
-
Associative: 결합법칙(a · b) · c = a · (b · c)
-
Identity element: 항등원a · e = a 를 만족시키는 항등원 e가 G에 존재한다
additive 그룹일경우 e = 0, multiplicative 그룹일경우 e = 1
-
Inverse element: 역원a · -a = e인 역원 a-1이 존재
Abelian group
-
Commutative: 교환 법칙G안의 모든 a와 b에 대해서 a · b = b · a 가 만족한다
Cyclic Group
G안에 어떤 원소 a가 있는데 G의 모든 요소들을 aⁿ 형태로 나타낼 수 있을 때 cyclic하다고 한다
이 때 a를 generator라고 부르고 그룹을 generate했다고함
모든 cyclic그룹은 abelian 그룹이다.
Exponentiation : 그룹 연산을 반복해서 적용
ex) a³ = a · a · a
Fields
어떤 집합과 연산 두 가지를 가지고 정의
(Group은 연산이 한 가지)
(GF로는 연산값을 mod했을 때 mod값이 전부 G에 포함인듯?
GF(7) = [ {0, ... , 6}, + mod 7, * mod 7])
- 그룹의 성질 1번 ~ 5번 모두 만족 (덧셈, 곱셈 모두에 대해서 abelian group 성립)
-
zero divisors 가 없음
만약 ab = 0이라면, a or b = 0이어야함
- 덧셈과 곱셈에서 분배 법칙이 성립한다
덧셈에서 그룹이라는 의미는 :
뺄셈 a - b는 a + (b의 역원)으로도 표현이 가능하다.
그룹의 모든 원소는 덧셈의 역원이 존재하므로 덧셈에서 그룹이라는건 뺄셈도 가능하다는 뜻
마찬가지로 곱셈에서 그룹이
라는 의미는:
그룹의 모든 원소는 곱셈의 역원이 존재하므로 나눗셈이 가능하다
즉, 필드는 덧셈, 뺄셈, 곱셈, 나눗셈이 그 집합을 떠나지않고 잘 정의가 되는 구조
유리수, 실수, 복소수는 모두 필드의 예시가 될 수 있으나
정수는 필드가 될 수 없다
why? 곱셈의 역원이 없는 수가 있기 때문
ex) 3의 곱셈의 역원은 1/3 (not 정수!!)
Finite fields (=Galois Field)
유한체 : 원소의 개수가 유한한 집합
Finite fileds의 원소 개수는 반드시 pⁿ개 이다 (p는 소수)
ex) GF (15) - (x), GF(7) - (o)
📌 GF(p) - Prime field
원소의 개수가 pⁿ개인데 n이 1
곱셈의 역원이 없는 정수들도 있지만
modulo와 서로소인수는 모두 곱셈의 역원이 있다
즉, modulo가 prime number라면 0을 제외한 모든 수(1~p-1)가 곱셈의 역원이 존재한다
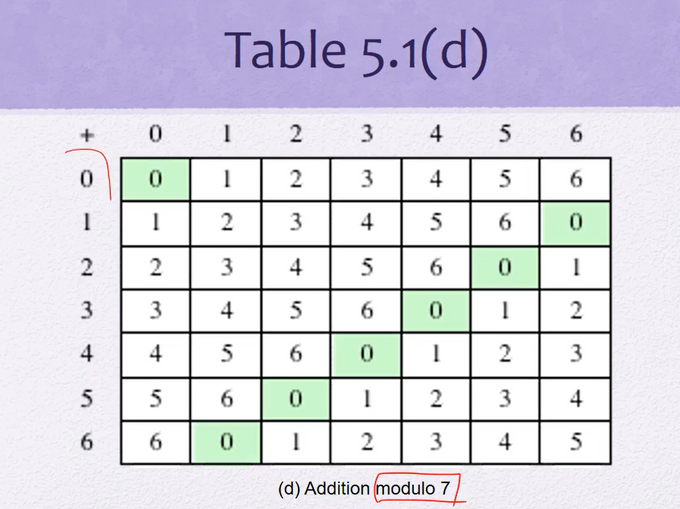
# 덧셈의 역원 (mod 7)
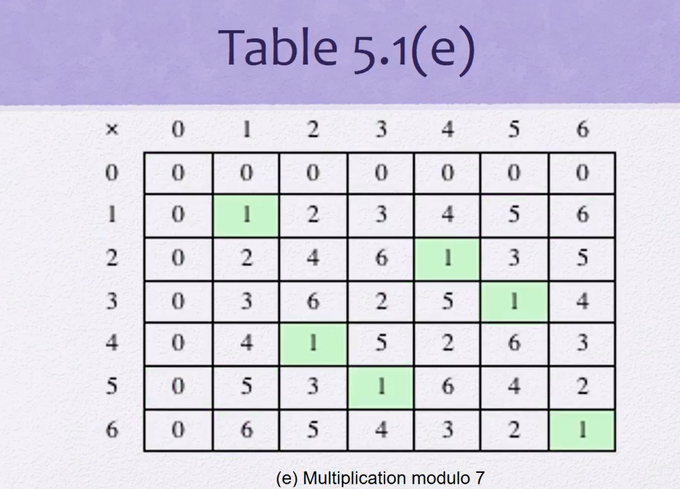
# 곱셈의 역원 (mod 7)
곱셈의 역원을 구하려면 Extended euclid algorithm을 써야함
곱셈의 역원 테이블을 보면 대칭임 (= Abelian group, 교환법칙이 가능하다는 뜻 )
GF(7) = [ {0, ... , 6}, + mod 7, * mod 7] <- 두 가지 연산을 모아서 필드가 정의됨
지금까지 얘기한 것은 Prime field!
GF(pⁿ) 인데 n = 1
이제 Binary field에 대해서 알아보자
GF(pⁿ) 인데 p = 2
Binary field를 쓰는 이유는?
DES같은 암호에서 입력이 64bit들어오면
AES는 128bit 8bit로 나눠서 사용(256가지 조합. 2의 8승)
256은 prime 아님 . 복잡해 ~~~
binary 쓰는게 맘 편함 ~ ㅎ 256가지 가지고 얍하려면 바이너리가 좋음
GF(2^8)
📌 Polynomial Divison
f(x) = q(X)g(X) + r(x)
r(x) = f(x) mod g(x)
만약 r(x)가 0, (= g(x)가 f(x)를 나눴다면)
g(x)|f(x)
g(x) 는 f(x)의 factor or divisor이라고 부른다.
irreducible
어떤 다항식 f(x) 가 필드 F에 대해서
irreducible하다f(x)를 차수가 더 작은 두 개 이상의 다항식 곱으로 나타낼 수 없다
즉, 인수분해 될 수 없음
prime과 비슷한 개념
📌 GF(2) = Binary Field
각 계수별로 mod 2 연산을 수행
mod 2를 하면 덧셈과 뺄셈이 같아진다 xor
x = -x = xor
📌 Polynomial GCD
두 다항식 a(x)와 b(x)의 GCD c(x)도 존재한다.
c(x)는 a(x)와 b(x) 둘을 나눌 수 있다
유클리드 알고리즘을 가지고 구할 수 있다
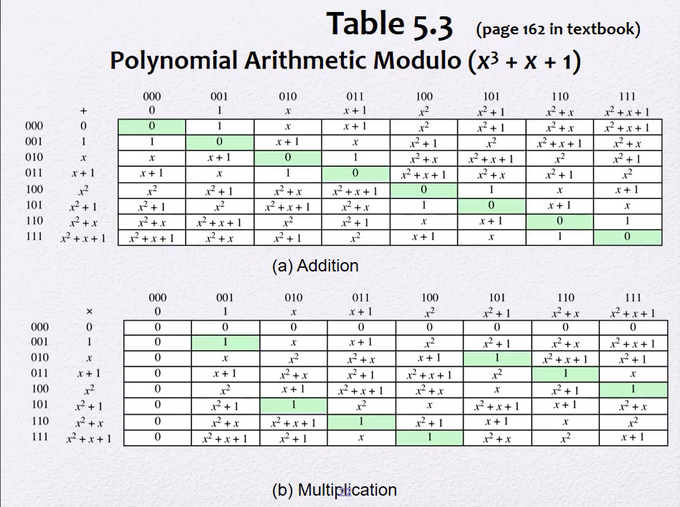
table 5.3은 GF(2³)
Addition mod - 덧셈의 역원
(mod 2 이므로 같은 것을 더하면 0이 된다.)
(x² + 1) 과 (x+1)을 더했을 때
x² + x + 2 (2는 mod2로 인해 사라진다)
결과 : x² + x
좀 더 기계적?으로 보자면
(x² + 1) = 101, (x+1) = 011
101과 011을 xor 연산하면 110. 즉, x² + x
xor하는 이유는 mod 2에서 덧셈 = 뺄셈 = xor
Multiplication mod
(x² + 1) 과 (x+1)을 곱했을 때 결과는 x³ + x² + x + 1
modulo x³ + x + 1 인데 모듈러보다 결과값이 크므로 모듈러로 mod해준다
(x³ + x² + x + 1) mod x³ + x + 1 는 x²
비트로 계산하려면
xor과shift를 사용한다!!(x² + 1) = 101, (x+1) = 011
101 * 011 = 1111 = (1000 + 111)
1000을 mod 1011하면 결과는 011!
(mod의 최고 차항을 mod로 나누면 최고차항을 뺀 나머지 다항식이 나머지가 된다. 예시로 x³ 을 x³ + x + 1로 나누면 나머지는 x + 1 )
1111 = (1000+111) = 011 + 111 = 100 즉, x²이다