AES
- 현대 Symmetic 암호는 Stream 암호와 Block암호로 구분된다
- Block암호에는 대표적으로 AES가 있다
- Advanced Encryption의 표준 DES : 56bit크기의 key 키 크기가 작아서 취약 키의 크기도 늘리고 성능 유지한게 AES
AES structure
128bit input ➡ Encryption ➡ 128 output
같은 input이라도 key값에 따라 output차이가 발생한다
궁극 목적
Bit randomizion effect
Block Cipher : finite field 사용 비트를 랜덤해보이도록 만들어서 최대한 인풋과 아웃풋의 연관관계가 없어보이게
- Field multiplication과 Field inversion을 통해 랜덤하게 변형 -> 그래서 finite field를 사용한다! 덧셈(뺄셈)은 반복하면 같아지는 효과가 있어서 제외
왜 덧셈은 반복하면 같아질까?
field : 사칙연산 덧셈 : randomize효과가 실질적으로 없음. 무작위로 바뀌지않고 계속 유지되는 성질 XOR 같은거 더하면 상쇄됨 연산을 반복한다고해서 복잡도가 올라가지않음
Rationale for Binary Field
n비트의 int는 2^n 개 표현 가능
그러나 모듈러 2^n은 field가 될 수 없음 ex) 2^3 = 8
-> GF(2^n)사용 GF안의 모든 polynomial들이 n비트 넘버를 표현
irreducible polynomial :
(GF기준으로 x2 + 1도 인수분해 가능.)
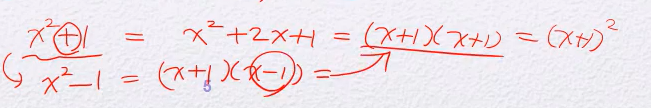
- 모드2 이므로 2x 추가
+와-가 같으므로x^2 - 1로 변환
State
AES에서 쓰는 기본 자료구조
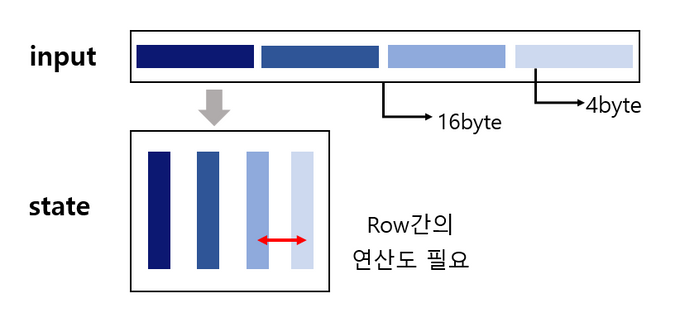
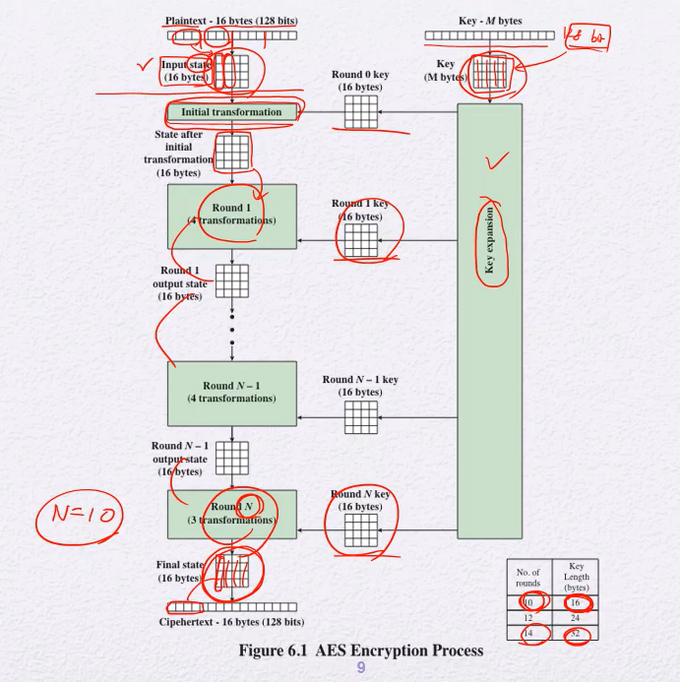
128bit : byte를 16개(4x4)의 형태이다 plain text, cipher text모두 128bit 단위로 암호화된다.
round key == subkey
round key의 비트는 똑같지만 개수가 많아짐 : expanded key
- key는 bit 수가 다른 여러가지 key가 있지만 plaintext는 항상 128bit로 고정이다
key size, 비트수가 커지면 round수도 커진다
각 round별로 키가 하나씩 사용된다
round수가 늘어나면 각 라운드마다 쓰일 서브키(라운드키) 개수가 증가한다
각각의 서브키 하나의 크기는 128bit로 고정되어있다. 개수만 늘어나는거임!
첫라운드전 한 번 + 각 라운드별로 서브키가 하나씩 사용됨
즉, 라운드키는 라운드 개수+1만큼 필요
서브키가 16byte 라운드가 10일경우 Expanded Key Size는
16*11 = 176
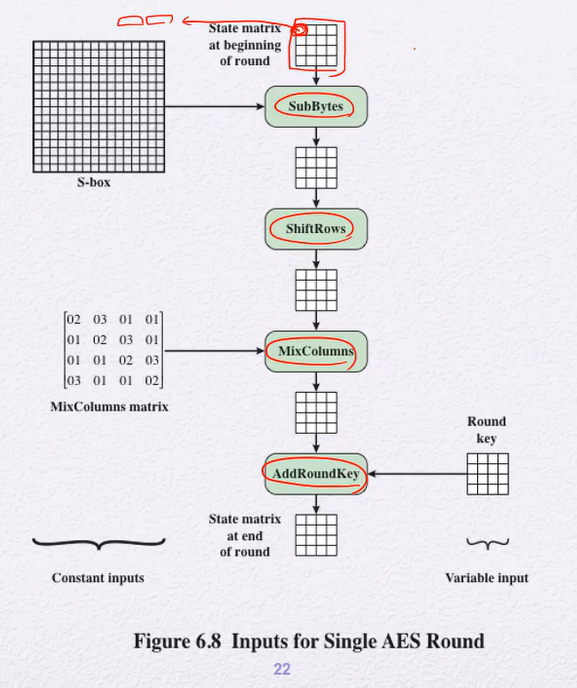
AES Encryption Process
State (4x4)
: 평문을 4x4형태에 맞게 열(세로)로 나열함
initial transformation
: 평문state와 key state를 xor
round : 4가지 프로세스를 반 ~ 복
(마지막 라운드에선 Mix Columns 수행을 안하긴 함)
key expansion(key schedule) = 서브키를 만들어내는 과정
Detailed Structure
- Feistel Cipher는 반으로 나눠서 반만 업데이트했지만 AES는 전체를 업데이트
- 결과적으로 AES에서 내부적으로 하는일은 전체적인 데이터의 블록(4x4)들을 substitution과 permutation을 이용해서 업데이트함
key가 128bit = 4 word, round가 10일 때,
필요한 라운드키는 4*11 word 총 word 44개가 필요
하나의 열에 8bit짜리 4개가 존재(4byte 한 줄) 이 4개를 합쳐서 하나의 w로
이를 w[0] ~ w[43]으로 표현할 것임
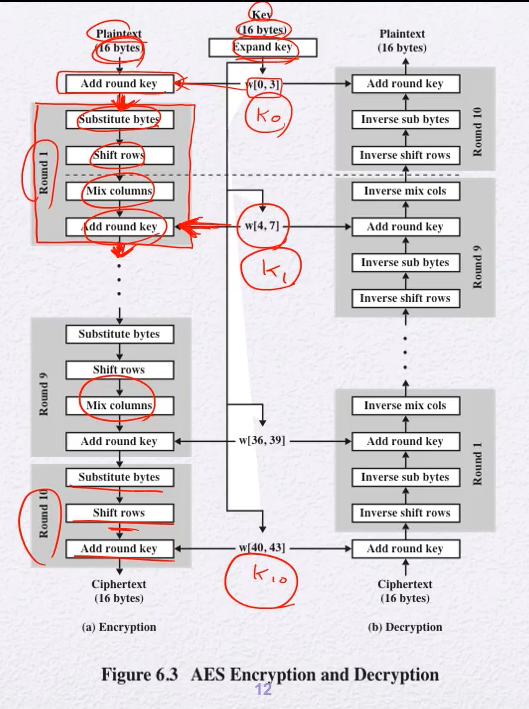구현상의 편의성때문에 마지막 프로세스에선 Mix columns없음
4개의 프로세스
3가지의 substitution과 1가지의 permutation으로 이루어진다
- Substitute bytes : (Substitution)
- Shift Rows : (Permutation)
- Mix Columns : 여러 라운드로 진행됨 (Substitution)
- Add Round Key (such as XOR) (Substitution)
Shift Row는 byte들의 위치를 바꿔주고 나머지 연산들은 byte들을 다른 byte로 대체해주는 역할을 한다
각 stage들은 역연산이 가능하다.
즉, 복호화할 때는 순방향이 아니라 역방향으로 진행한다
얘는 암호화 과정과 복호화 과정이 똑같지않음
입력의 일부분이 출력의 여러부분에 분산해서 영향을 미치도록 만들면서 입력과 출력간의 관계가 잘 드러나지않게 하는 것이 최종 목적
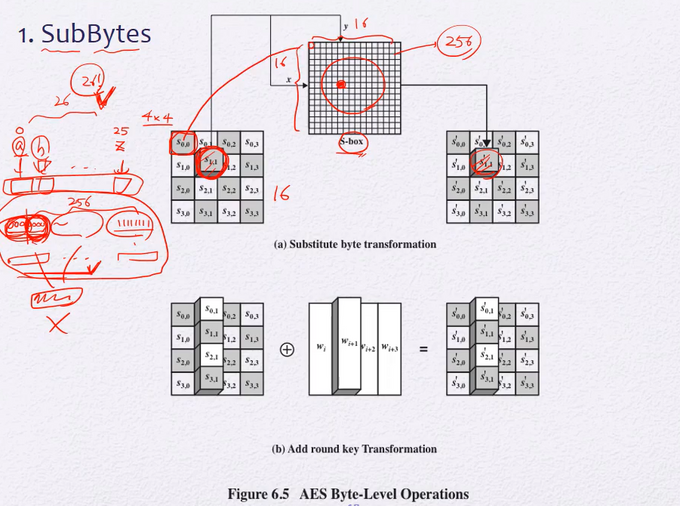
1. Substitute Bytes
byte단위로 업데이트, 치환을 해준다.
4x4 byte(128bit)중 하나의 byte를 S-box라고 함
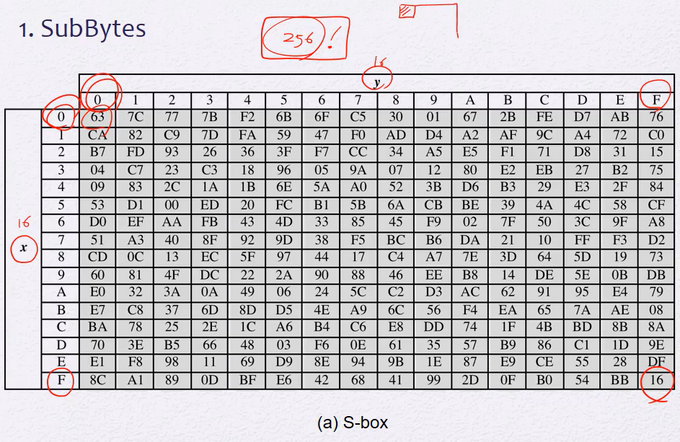
S-box각 바이트들을 다른 바이트로 대체해주는 규칙
모든 S-box사용자들이 같은 규칙을 씀(key의 일부가 아니라 정해진 방법) :
서로 다른 8bit가 다른 8bit와 1대1연결되어있다(역연산이 가능해야하므로)
ex)
8bit가 00000000일 경우, x : 0000 / y : 0000으로 보고 63을 매칭시켜준다.
4x4의 state의 각 byte, 총 16개의 byte를 S-box에 보낸다
16개의 byte를 독립적으로.
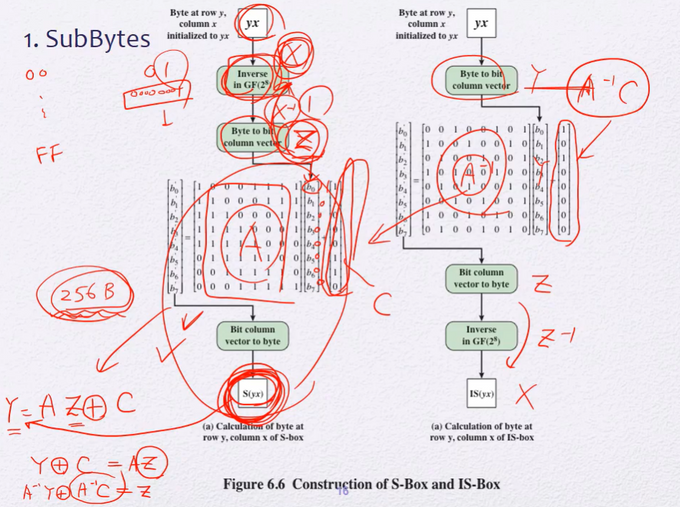
😨 S-box 연산과 역연산
- 😨 Inverse in GF(2^8) : 각 byte에 대한 역원을 구한다.
00000000 : 다른 수들은 모두 곱셈의 역원이 있지만 0의 역원은 0이므로 0은 그대로 0
- 😨 Byte to bit column vector
s-box안의 bit를 b7(최상위비트)~b0(최하위비트)에 차례대로 넣는다
만약 00000001을 넣어야한다면
b7부터 차례대로 00000001이 들어간다 (b0 = 1)
- 😨 행렬곱한다!
00000000이 들어갔다고 칠 때
우선 00000000 과 옆의 행렬을 곱해서(bn * 각 행의 n번째원소) 차례대로 (1)b0~b7에 다시 넣는다 (지금은 0이 들어갔으므로 행렬곱해도 다 0으로 나옴)
옆에 bit (2)11000110 를 GF에서 mod 2 하던것처럼 xor
(1)의 bit(이 예시에서는 00000000)와 (2)의 앞 bit부터 xor시킨다
- 😨 bit column vector to byte
결과값은 01100011으로(최상위 비트부터 읽는다) 0을 S-box에 통과시키면 63이 된다.
예시 하나 더!
- Inverse in GF(2^8)
인풋이 x: 0000, y: 0001일때, 1의 역원은 1이므로 00000001이 들어간다
00000001을 최상위 비트(b7)부터 담는다
- Byte to bit column vector
b0 |
b1 |
b2 |
b3 |
b4 |
b5 |
b6 |
b7 |
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
- 행렬곱
b0~b7이 10000000이고, 행렬의 첫 번째 행이 10001111 이라면_
bn과 n번째 원소를 곱하고
곱한 결과들을 모두 더해서 bn에 넣는다
이걸 8번 수행(b0~b7에 모두 집어넣음)
10000000 * 10001111 = 1 + 0 + ...+0 = 1, b0에는 1이 들어간다
- 옆에 bit
11000110과 b0~b7을xor연산한다
11000110 xor 11111000 = 00111110
- bit column vector to byte
00111110을 최상위비트(b7)부터 읽는다 : 01111100
01111100을 16진수로 읽으면 7C 즉 output은 7C이다.
입력이 X(00~256), X의 iverse를 Z, 행렬을 A라고 할 때,
Z를 bit 벡터로 표현한뒤 A를 곱하고 그 결과에 상수 C를 더한다.
ZA + C = Y(00~FF)(결과)
반대로 역연산할경우 6과 3을 사용해 00임을 알 수 있다
😨 역연산
역연산을 하려면? Y가 들어갔을 때 Z가 나오게 하면 된다
Y - C = ZA
-A (Y - C) = Z (사실 +나 -나 동일, -A는 A의 역행렬)
인풋과 아웃풋의 상관관계를 예측하기 어려운 암호가 좋은 암호
-> linear 함수를 사용 자제. linear할 경우 몇 개의 p-c 쌍으로 연립방정식을 사용해 암호를 풀 수도 있음.
그래서 nonlinearity인 곱셈이나 곱셈의 역원 사용
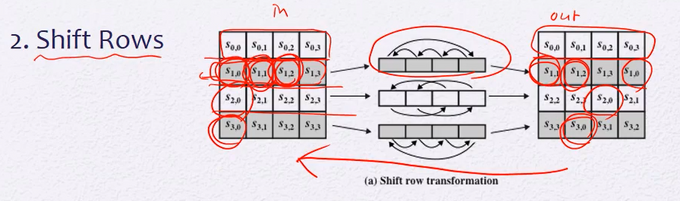
2. Shift Rows
plaintext를 4byte씩 잘라서 column으로 나열함
나열한 column끼리만 연산하면 잘 안 섞임
그래서 SR 필요
Row, 행만 움직임. 열은 움직이지않음
- 첫 번째 행은 안움직임
- 두 번째 행은 왼쪽으로 한 칸
- 세 번째 행은 왼쪽으로 두 칸
- 네 번째 행은 왼쪽으로 세 칸 (= 오른쪽으로 한 칸)
동작 자체는 간단하나 column에 대한 연산만 반복하면 잘 안섞임
3. Mix Columns
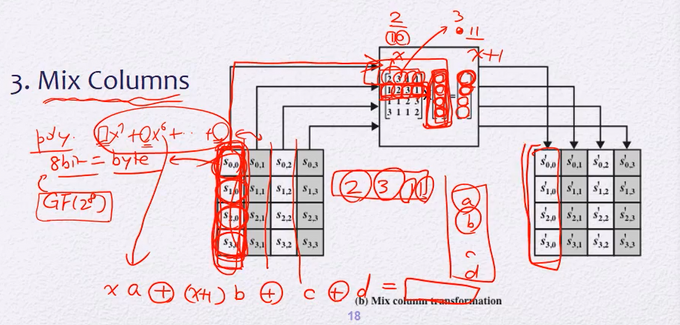한 컬럼의 일 부분이 다른 컬럼의 여러 부분에 영향을 미치게 한다
마찬가지로 Columns만 움직임
cell하나가 하나의 byte
8bit를 다항식의 개수로 본다.(GF(2^8)의 폴리노미얼로 표현되는 원소가 된다)
열에 있는 네 개의 cell과 주어진 행렬과 행렬곱 시킨다
행렬의 수는 GF(2)로 표현된 다항식으로 만약 cell이 abcd고 곱할 행렬의 행이 2 3 1 1 이라면
행렬곱 결과는 xa + (x+1)b + c + d 가 된다
일종의 substitution연산
이에 대한 역연산은 결과값에 역행렬을 곱해주면 입력값이 나온다
4. Add Round Key
단순히 xor : 128bit의 State를 128bit 라운드키와 xor
그러나 Round key expansion은 복잡
전체적인 프로세스
Add Round Key 전에는 input이 같으면 모두 똑같이 나오지만 Round key에 따라 같은 input이더라도 다른 output이 나온다.
AES의 안전성을 보장하는 가장 큰 요인은 key이다
ShiftRows로 인해
- 첫 번째 행은 이동 안함.
- 두 번째 행은 오른쪽으로 세 칸(=왼쪽으로 한 칸) 이동
- 세 번째 행은 오른쪽으로 두 칸 이동
- 네 번째 행은 오른쪽으로 한 칸 이동
바뀐 한 byte로 인해 MixColumns를 하면 더 다른 다항식이 만들어진다.
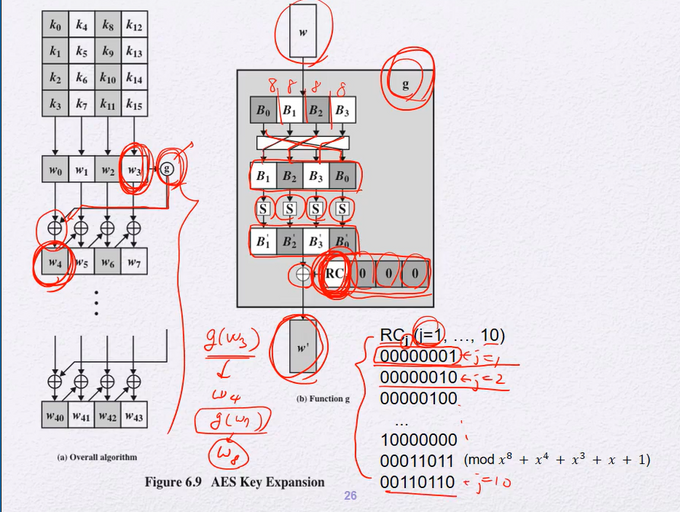
key expansion
nonlinearity
Diffusion: 어떤 한 비트의 변화가 여러 비트에 영향을 미치게 만드는 효과
w0 ~ w3이 K0 w4 ~ w7이 K1
함수 g
입력받은 word를 8bit씩 쪼개 4byte로 만든다
위치를 그림과 같이 이동시키고
S-box를 사용해 치환한다
치환한 값을 어떤 상수(4byte)와 xor한다
AES의 장점
안전성도 안전성이지만 여러가지 프로세스적면에서 효율적
- 8bit의 기본 연산을 사용하는 cpu에서 잘동작한다.
- xor이나 shift 오퍼레이션등 간단한 연산 사용
우리가 사용하는건 32-bit processor인데 8bit연산이 효율적일까?
32bit에서도 잘동작함.
BS, SR, MC의 세 오퍼레이션을 하나로 합칠수있음
4table lookups + 4XORs로 끝낼 수 있다